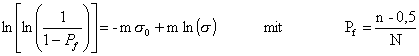
|
(7) |




Aus dem erhaltenen Kraft-Weg-Diagramm wurde unter Berücksichtigung des mittleren Faserquerschnitts, der Einspannlänge, der Traversengeschwindigkeit und der Schreibergeschwindigkeit das Nennspannungs-Totaldehnungs-Diagramm erhalten, aus dem man die Zugfestigkeit, die elastische Dehnung und den Elastizitätsmodul nach Gleichung (6) berechnen kann. Gleichung (6) setzt die Gültigkeit des Hook'sche Gesetzes voraus, was bei der untersuchten Faser gegeben ist.
| s = E e | (6) |
| Tabelle 3: Parameter zur Berechnung der Nennspannungs-Totaldehnungs-Diagramme. | ||
| Traversengeschwindigkeit, mm/min | ||
| Schreibergeschwindigkeit, cm/min | ||
| Mittlerer Faserausgangsquerschnitt A0 | ||
| Mittlerer Faserdurchmesser d, mm | ||
| Einspannlänge l0 | ||
Sprödbrechende Fasern weisen ein statistisches Versagensverhalten auf, was zu großen
Schwankungen der erhaltenen Meßwerte führt. Zur Ermittlung der Ergebnisse aus den einzelnen
Meßwerten wurde deshalb eine statistische Auswertung nach Weibull [66, 67], welche im Anhang
A.2 beschrieben ist, durchgeführt. Der so
erhaltene Weibullparameter s0
ist ein Maß für eine 63,2%-ige Versagenswahrscheinlichkeit Pf der Faserprobe
bei einer bestimmten Zugfestigkeit s.
Der Weibullparameter m gibt die Streuung der Meßwerte um s0
an (Gleichung (7)):
Zur Auswertung wurden die Werte für die Zugfestigkeit s aufsteigend sortiert, die einzelnen Punkte nach Gleichung (7) berechnet und in ein Diagramm eingezeichnet. Der Weibullparameter m entspricht der Steigung der Ausgleichsgeraden, der Normierungsfaktor s0 dem Schnittpunkt der Ausgleichsgeraden mit der y-Achse (s = s0).



